7757. Square
Jian-Jia
has a piece of metal material and he wants to cut a square out of it. The
material consists of n by n unit grids and Jian-Jia can only cut
the material along grid boundary. Each grid is either usable or defective, and
Jian-Jia wants to cut the largest possible square from the material without any
defective grids. After determining the maximum size of the square, Jian-Jia
also wants to know how many ways he can cut the largest square from this
material. Finally Jian-Jia will report the product of the maximum size and the
number of possible ways.
Consider
the 6 by 6 material in the following figure. The black grids are defective. The
largest square Jian-Jia can cut from the material is 3 by 3, and there are two
ways to cut it - the red square and the green square. Jian-Jan will report the
product of 3 and 2, which is 6.

Your
task is to find the size of largest squares in the material, count the number
of ways to cut them, and report the product of the size and the number.
Input. First line
contains the size of the material n
(1 ≤ n ≤ 1000). Each of
the next n lines contains n integers. A 1 means the grid is useful
and a 0 means the grid is defective.
Output.
Print one integer – the product of the size of largest square
in the material, and the number of possible locations in the material.
|
Sample
input 1 |
Sample
output 1 |
|
6 1 0 1 0 1 0 0 1 0 1 0 1 1 0 1 0 1 0 0 1 0 1 0 1 1 0 1 0 1 0 0 1 0 1 0 1 |
18 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
6 0 1 1 1 1 0 1 0 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 |
6 |
SOLUTION
dynamic programming
Algorithm analysis
Declare array dp, where dp[i][j] contains the size
of the biggest square that can be cut from the rectangle (0, 0) – (i, j)
with condition that the cell (i, j) belongs to this square.
Let array m contains the input data.
If m[i][j] = 0 (the part of grid is defective), then
dp[i][j] = 0.
Let
m[i][j] = 1. Consider two cases:
1.
m[i – 1][j] = m[i][j
– 1] = k. Then the value of dp[i][j]
depends from the value of m[i – k][j
– k]:
·
if m[i – k][j – k]
= 1, then all the square (i – k, j
– k) – (i, j) will contain ones
only and dp[i][j] = k + 1.
·
if m[i – k][j – k]
= 0, then dp[i][j] = k.
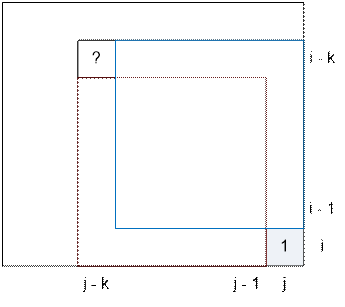
2.
m[i – 1][j] ≠ m[i][j – 1]. Then dp[i][j] = min(dp[i – 1][j], dp[i][j – 1]) + 1.
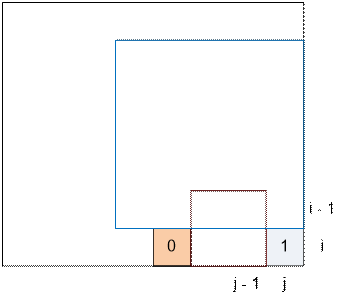
Summarizing
the said above we can be see that
dp[i][j]
= min(dp[i – 1][j], dp[i][j – 1], dp[i – 1][j – 1]) + 1
Example
Consider the second test
case. Let’s fill dp array for it.
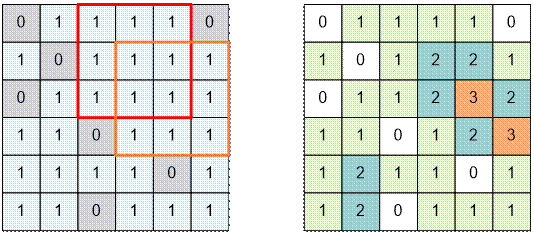
There are 2 largest
squares of size 3 * 3. The product of the size of the largest square by the
number of its locations is 3 * 2 = 6.
Algorithm realization
Declare the two-dimensional array dp.
#define MAX
1010
int
dp[MAX][MAX];
Read
the value of n. The variable size keeps the size of biggest square, cnt keeps the number of times it appears
in the material. Initialize array dp with zeroes.
scanf("%d", &n);
memset(dp,0,sizeof(dp));
size
= cnt = 0;
Calculate
the values of dp in ascending order of rows, and the values in each row in ascending
order of columns.
for(i = 1; i
<= n; i++)
for(j = 1; j
<= n; j++)
{
scanf("%d",&val);
Let all the values of array dp till the square (i, j)
are found. Read the current value val
= m[i][j] (we do not contains the input matrix in the memory, we read and
process it on fly). Since we initially zeroed the array dp, so when val = 0 the value of dp[i][j]
stays equal to 0.
if (val ==
1)
{
dp[i][j] =
min(min(dp[i][j-1],dp[i-1][j]),dp[i-1][j-1]) + 1;
Recalculate the values size and cnt for the
current square of the size dp[i][j].
if
(dp[i][j] == size) cnt++;
if
(dp[i][j] > size) {size = dp[i][j]; cnt = 1;}
}
}
Print the answer.
printf("%lld\n",1LL * size * cnt);